LUMIÈRE - Optique

LUMIÈRE - Optique

Il est difficile de séparer nettement les notions de lumière et d’optique. La lumière, évidence sensible, apparaît communément comme première par rapport à l’optique, science dont l’objet est l’étude de la lumière et qui englobe toutes les techniques liées à son utilisation. Il est donc opportun d’insister ici sur les difficultés conceptuelles soulevées depuis toujours par la compréhension de la nature de la lumière et de réserver aux articles de l’ensemble OPTIQUE le soin de décrire les moyens mis en œuvre pour la maîtriser.

Après les méandres du «feu visuel», des ondes lumineuses se propageant à travers l’«éther» et des corpuscules de l’école newtonienne (cf. LUMIÈRE – Histoire des idées), les conceptions actuelles reposent sur la connaissance des phénomènes développés dans les articles suivants de l’ensemble LUMIÈRE. En effet, la statut stable de théorie achevée dont jouit l’électromagnétisme rejaillit sur toute la description de la propagation de la lumière, à travers le vide comme à travers les milieux matériels; en revanche, l’émission et la détection de lumière ne peuvent être appréhendées que dans le cadre de la mécanique quantique, aux frontières encore floues (cf. mécanique QUANTIQUE et optique QUANTIQUE), et rares sont encore les physiciens pouvant se vanter d’avoir une idée entièrement satisfaisante de ce qu’est un photon.

Le présent article se propose de délimiter le domaine de l’optique par référence aux principales caractéristiques de la lumière.

La théorie de la lumière précise et nuance la loi de propagation rectiligne de la lumière, dont les limites sont mises en évidence par quelques expériences classiques. Ainsi, la formation d’image par un miroir, la rupture apparente du bâton plongé obliquement dans l’eau, la conduction de la lumière par les fibres optiques conduisent aux phénomènes de réflexion et de réfraction. Les instruments d’optique les plus répandus tels que les lunettes, les appareils photographiques, les télescopes et les microscopes sont l’application directe de ces phénomènes dont l’interprétation amène à introduire une vitesse de propagation variable selon le milieu traversé. La décomposition de la lumière blanche par un prisme ou dans un arc-en-ciel et sa synthèse à partir des secteurs colorés du disque tournant de Newton amènent à concevoir la notion de couleur pure. L’image d’un lampadaire lointain observé la nuit à travers des rideaux, le saisissant relief restitué par un hologramme, sans remettre en cause la loi de propagation rectiligne à travers un milieu homogène, obligent à admettre son insuffisance: ces phénomènes de diffraction, tout comme ceux d’interférences illustrés, par exemple, par les irisations des bulles de savon, trouvent leur interprétation dans le modèle ondulatoire de la lumière, où chaque couleur pure est décrite comme une « vibration monochromatique» variant sinusoïdalement dans le temps avec une période de l’ordre de 2 . 10^-15 s. La célèbre observation de Malus (1809) examinant la double réfraction d’un cristal de spath d’Islande à l’aide de la lumière réfléchie par les vitres du palais du Luxembourg a contribué à introduire la notion de polarisation de la lumière et celle de transversalité des ondes lumineuses; elle a amené à envisager la lumière comme une onde électromagnétique constituée d’un vecteur champ électrique et d’un vecteur champ magnétique perpendiculaires à la direction de propagation. Les propriétés de récepteurs répandus, comme ceux qui utilisent l’effet photoélectrique ou tout simplement la plaque photographique, sont décrites de façon cohérente en faisant appel au concept de photon, «grain élémentaire» de lumière, de masse nulle, d’énergie et d’impulsion proportionnelles à sa fréquence. Ainsi l’évolution de la théorie de la lumière a-t-elle fait éclore au début de ce siècle la notion de «dualité onde-corpuscule», si contraire à l’intuition, étendue ensuite aux particules de masse non nulle, et qui a plongé dans la perplexité plusieurs générations de physiciens.

Chaque source n’émet que dans une région limitée de l’ensemble des fréquences et chaque récepteur n’est sensible qu’à une certaine bande spectrale: ainsi, les fréquences absorbées par les pigments rétiniens définissent le domaine de la lumière visible. Les fréquences des ondes visibles s’étendent sur un domaine relativement étroit (autour de 5 . 10¹⁴ Hz), alors que celles des ondes électromagnétiques couvrent un spectre beaucoup plus étendu (fig. 1). Les ondes non visibles des régions infrarouge et ultraviolette présentent avec les ondes visibles une unité de propriétés telle qu’il serait anormal de leur refuser le nom de «lumière». Toute restriction dans l’utilisation de ce nom pour une onde électromagnétique porte en fait une grande part d’arbitraire et masque la continuité parfaite des phénomènes observés sur tout le spectre, des ondes hertziennes aux rayons gamma.

L’émission de lumière est caractérisée non seulement par son spectre et ses paramètres photométriques ^{[cf. PHOTOMÉTRIE]}, mais aussi par le processus physique mis en jeu: désexcitation spontanée des atomes ou des molécules après une excitation thermique dans une lampe à incandescence, choc électronique dans les lampes à décharge, absorption de lumière en photoluminescence, désexcitation stimulée dans les lasers, rayonnement de charges en mouvement accéléré dans quelques cas comme le rayonnement synchrotron.

La détection de la lumière ne repose en dernière analyse que sur deux phénomènes: l’échauffement consécutif à l’impact du photon qui produit une agitation supplémentaire dans la matière composant le récepteur et l’arrachement sélectif par le photon d’un électron projeté par effet photoélectrique d’un état à un autre.

La vitesse de la lumière varie avec le milieu traversé et, pour chaque milieu, avec la fréquence, sauf dans le vide. Le rapport de la vitesse dans le vide à la vitesse dans un milieu pour une fréquence donnée définit l’indice de réfraction de ce milieu pour cette fréquence. La vitesse de la lumière dans le vide est une constante fondamentale dont l’importance dépasse le champ de l’optique car, en relativité, elle apparaît comme la vitesse limite de toute propagation d’énergie et de signal. Sa mesure a constamment gagné en précision, depuis qu’il a été établi, au XVII^e siècle, qu’elle n’est pas infinie, jusqu’au jour de 1983 où l’évolution de la métrologie l’a privée de son sens en utilisant sa valeur, désormais immuable, pour définir le mètre.

1. La théorie de la lumière

Au terme d’une évolution complexe (cf. LUMIÈRE – Histoire des idées), la description scientifique actuelle de la lumière fait intervenir la mécanique quantique et les photons, ou plutôt les «quantons» (cf. mécanique QUANTIQUE), qui, si on essaie de les décrire à l’aide des concepts familiers à notre intuition, procèdent autant de l’onde que de la particule. Cette description n’est pas un paradoxe, car nos sens ne nous fournissent aucune indication sur la façon d’aborder la physique du microscopique. Même si les concepts d’onde et de particule ne conviennent pas parfaitement pour décrire la lumière, ils sont suffisamment bien définis et connus pour nous aider dans l’évocation des différentes propriétés de la lumière.

Optique géométrique

La réflexion sur une surface de discontinuité et la réfraction lors de la traversée d’une telle surface ainsi que le comportement de la lumière dans un milieu d’indice de réfraction continu mais progressivement variable font l’objet de l’optique géométrique (cf. OPTIQUE – Principes physiques). La loi la plus connue est la propagation rectiligne de la lumière dans les milieux homogènes, avec pour concept fondamental le rayon lumineux. Il est difficile d’accorder à l’optique géométrique le statut de «théorie de la lumière», car elle ne propose aucune interprétation de la nature de la lumière ni du rayon lumineux. En revanche, elle apparaît comme un cas limite aussi bien de l’approche ondulatoire que de l’approche corpusculaire (cf. infra ): l’impossibilité d’isoler un rayon lumineux par deux diaphragmes arbitrairement fins fait appel à l’optique ondulatoire, alors que la nature discontinue de l’interaction entre lumière et matière relève de l’optique corpusculaire; le domaine de validité de l’approximation géométrique est en fait très étendu.

Approche ondulatoire

Les phénomènes de diffraction et d’interférences, étudiés avec attention vers le début du XIX^e siècle, semblèrent inexplicables dans les termes corpusculaires chers à l’école newtonienne, et une théorie ondulatoire s’imposa, à la suite des travaux de Young (1780) et de Fresnel (1818). Il fut dès lors possible d’exprimer l’éclairement d’un écran recevant plusieurs ondes monochromatiques comme la moyenne dans le temps du carré de leur somme (cf. INTERFÉRENCES LUMINEUSES et LUMIÈRE – Diffraction). Les fondateurs de cette théorie, entraînés par la comparaison des ondes lumineuses avec des ondes élastiques, mais sachant que la lumière se propage même dans le vide, avaient imaginé un milieu hypothétique, l’éther , qui leur semblait nécessaire «pour attribuer un sujet au verbe vibrer». Si l’introduction par Maxwell de l’électromagnétisme (1872) permit de prévoir la vitesse de propagation dans le vide ou dans l’«éther», restait posée la question épineuse du «repère absolu» par rapport auquel l’éther serait au repos. Le résultat de l’expérience célèbre de Michelson et Morley (1887), qui cherchèrent en vain à déceler optiquement le mouvement de la Terre par rapport à l’éther, fut confirmé par tous les essais ultérieurs. Mais c’est surtout l’attrait théorique et formel de la notion de relativité ^{[cf. RELATIVITÉ]} qui conduisit Einstein en 1905 à nier les notions de repère absolu et d’éther et à admettre que la vitesse de la lumière dans le vide est la même dans tous les référentiels galiléens; on reviendra à la fin du présent article sur cette vitesse.

La théorie électromagnétique de Maxwell a complété la théorie ondulatoire en introduisant deux grandeurs vectorielles qui sont les grandeurs vibrantes: la lumière apparaît, dans le cas d’une onde monochromatique, comme constituée d’un champ électrique et d’un champ magnétique variant sinusoïdalement avec le temps. Les études rigoureuses de diffraction font intervenir le calcul de ces champs par résolution complète des équations de Maxwell. Pour une onde plane, les deux champs, proportionnels, se propagent ensemble par ondes transversales, leurs directions étant constamment normales entre elles ainsi qu’à la direction de propagation.

La plupart des effets de la lumière sont attribuables au vecteur électrique. C’est ce que justifie, par exemple, l’expérience d’ondes stationnaires de Wiener décrite à l’article INTERFÉRENCES LUMINEUSES.

La théorie électromagnétique indique que la vitesse de propagation est, dans le vide,

et la longueur d’onde dans le vide, correspondant à la fréquence 益 est:

Dans un milieu matériel, la vitesse devient: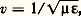

猪⁰, 猪, 﨎⁰, 﨎 étant respectivement les perméabilités et permittivités du vide et du milieu définies en électricité et magnétisme.

On a, par suite:

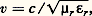猪^r = 猪/ 猪⁰ et 﨎^r = 﨎/ 﨎⁰ étant la perméabilité et la permittivité relatives du milieu. L’indice de réfraction de celui-ci est donc:

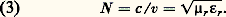猪^r , aux fréquences optiques, est pratiquement égale à 1; 﨎^r , par contre, varie avec la fréquence dans tous les milieux non vides: on parle de dispersion des ondes électromagnétiques; l’effet de la conductivité électrique du milieu peut, dans un calcul en notation complexe, être incorporé à 﨎^r : cette dernière devient un nombre complexe dont la partie imaginaire rend compte du phénomène d’absorption (cf. LUMIÈRE – Dispersion et absorption).

La matière n’étant pas continue, mais formée d’atomes et de molécules, on a été conduit à regarder les échanges entre ceux-ci et les ondes électromagnétiques comme semblables à ceux qui existent entre les ondes de la radioélectricité et les antennes émettrices et réceptrices les plus simples. Quand le milieu est un corps pur à l’état de gaz ou de vapeur sous faible pression, l’expérience montre que les radiations émises ou absorbées forment un spectre de raies; la théorie électromagnétique admet que l’atome, ou la molécule, qui émet une radiation déterminée contient des charges électriques oscillant sinusoïdalement, avec une fréquence mécanique égale à la fréquence optique.

Cette représentation conduit à regarder l’absorption comme un phénomène de résonance : l’onde exerce sur les particules chargées, contenues dans les molécules, des forces qui les mettent en vibrations forcées. De l’énergie est cédée par l’onde à l’oscillateur; elle passe par un maximum lorsque leurs fréquences sont voisines. Hors des régions d’absorption, la synchronisation des oscillateurs moléculaires permet d’expliquer la réfraction et sa dispersion, ainsi que la diffusion et la double réfraction. Il est de même facile d’interpréter, en première approximation, l’action des champs électriques ou magnétiques sur les spectres d’émission et d’absorption ainsi que sur la biréfringence. Cette description classique de la dispersion et de l’absorption ne permet pas de rendre compte de façon convenable de l’état des charges oscillantes. Si l’on considère la totalité du spectre d’un atome, et non plus une seule de ses raies, la distribution de l’ensemble ne s’accorde pas avec ce qu’on doit attendre d’oscillateurs périodiques (présence d’harmoniques dont les fréquences sont des multiples simples d’une même valeur fondamentale). De plus, l’émission de rayonnement entraîne une perte continue d’énergie mécanique de l’oscillateur, incompatible avec la stabilité de l’atome et l’émission de lumières quasi monochromatiques. On a dû renoncer à appliquer aux mouvements des constituants des molécules les lois de la mécanique newtonienne; il a fallu élaborer une mécanique quantique , qui fournit d’ailleurs une explication cohérente d’un grand nombre de faits de la physique et de la chimie atomiques.

Seule la mécanique quantique fournit une description cohérente de ces phénomènes. Il se trouve toutefois que les résultats quantiques concernant la dispersion et l’absorption peuvent être mis en accord avec les formules classiques, en modifiant l’interprétation des paramètres qui y interviennent. La théorie électromagnétique, dont la mise en œuvre est relativement intuitive et simple, rend encore de précieux services.

Approche corpusculaire

Il est très difficile d’expliquer en termes d’optique ondulatoire des phénomènes comme la détection de la lumière grâce à l’effet photoélectrique, ou, dans une moindre mesure, le noircissement d’une émulsion photographique: les émulsions photographiques contiennent des «grains», très petits cristaux ioniques de bromure d’argent, qui deviennent noirs sous l’action du révélateur, par suite d’une libération d’atomes d’argent métallique à l’endroit où la lumière les a impressionnés. Or, si le temps de pose est assez faible, le nombre de grains noirs (qui se traduisent par des blancs sur l’image «positive», comme le montre la figure 2) est bien inférieur à celui des cristaux contenus dans l’émulsion. Il augmente proportionnellement à ce temps de pose, tant que le noircissement est assez inférieur à sa valeur maximale. Si la lumière avait la structure continue que laisserait prévoir l’analogie avec les ondes acoustiques (par exemple), tous les grains, supposés identiques, recevant un même éclairement seraient simultanément soumis à son action. On doit donc admettre que l’énergie rayonnante est captée sous forme de corpuscules, qu’on a appelés quanta de lumière ou photons .

La théorie quantique de la lumière, développée en 1906 par Einstein, a son origine dans les travaux de Planck qui, dès 1900, pour expliquer les lois du «corps noir» (cf. Incandescence , in chap. 3), avait indiqué que les échanges d’énergie entre matière et rayonnement ne peuvent se faire que par multiples entiers d’un quantum W = h 益, proportionnel à la fréquence 益 émise ou absorbée.

On verra plus loin, dans Optique quantique (cf. aussi l’article BOHR), comment Niels Bohr a utilisé cette théorie pour l’interprétation des spectres atomiques et moléculaires. La valeur actuellement admise pour la «constante de Planck» h est, à 5.10^-6 près, 6,626 075 5 憐 10^-34 J.s. De cette donnée, on déduit aisément quelques ordres de grandeur importants: à l’infrarouge d’une longueur d’onde dans le vide proche de 1 猪m correspond, pour le photon, une énergie W = 1,24 eV; on utilise comme unité, pour évaluer l’énergie d’un photon, l’électron-volt (eV), énergie qu’acquiert un électron accéléré par une différence de potentiel de 1 volt: 1 eV = 1,602.10^-19J; un éclairement de 20 lux, convenable pour un travail de bureau, fourni par une source lumineuse de longeur d’onde dans le vide voisine de 0,55 猪m, est obtenu par l’impact d’environ 2 . 10¹⁷ photons par mètre carré et par seconde transportant une énergie de 0,1 W/m².

Optique quantique

La diffraction de la lumière et les interférences lumineuses sont régies avec précision par l’optique électromagnétique; l’interaction entre lumière et matière est décrite par l’approche corpusculaire. Le comportement de la lumière est décrit de façon commode par l’optique géométrique: ses rayons lumineux sont les trajectoires suivies par l’énergie des ondes lumineuses ainsi que les chemins le long desquels on peut détecter les photons. Lorsque l’optique géométrique s’avère insuffisante, les descriptions ondulatoire et corpusculaire s’accommodent le plus souvent d’une simple juxtaposition: ainsi l’analyse d’une figure d’interférences ou de diffraction par un récepteur est-elle parfaitement décrite par la détection d’un nombre de photons proportionnel à l’éclairement prévu par l’optique ondulatoire. On a effectué une série d’expériences où s’impose une approche quantique globale qui repose sur les bases ardues de l’électrodynamique quantique (cf. optique QUANTIQUE). C’est le cas des expériences d’interférences à un seul photon: l’appareil a un flux extrêmement faible et son montage assure que la présence simultanée de deux photons ou plus est très improbable; la figure d’interférences est alors observable si aucun détecteur n’observe «par laquelle des deux voies de l’interféromètre est passé le photon».

Ce tableau de la théorie de la lumière montre à quel point elle est liée à la physique tout entière: le développement de la physique, jusqu’à ses aspects les plus récents élaborés sur les bases de la relativité et de la mécanique quantique, repose en grande partie sur l’étude de la lumière.

2. Le spectre de la lumière

Toutes les propriétés de la lumière évoquées dans le premier chapitre se manifestent aussi bien dans le domaine visible que dans le domaine invisible du spectre électromagnétique. Pour étudier la composition d’une lumière, on peut la concentrer sur une fente fine dont on forme, à l’aide d’un système dispersif (à prisme, par exemple), un ensemble d’images dues aux diverses composantes: elles constituent le spectre de la lumière étudiée. Ce spectre peut être continu, c’est-à-dire faire apparaître une suite ininterrompue d’images; sinon, c’est un spectre de raies ou de bandes (une seule raie pour une lumière monochromatique). Un étalonnage du dispositif donne les valeurs des longueurs d’onde en fonction des positions de raies.

Les lumières blanches, telles que celles du Soleil, sont constituées de radiations simples s’échelonnant du violet au rouge, comme l’indique la figure 1. L’étude des lumières colorées complexes se trouve à l’article COULEUR.

Les limites du spectre visible varient un peu selon les observateurs et selon l’intensité du faisceau observé. On peut admettre conventionnellement que le domaine des radiations infrarouges (qui sont dites proches, moyennes ou lointaines par rapport au spectre visible) s’étend entre les longueurs d’onde 0,78 猪m et 1 mm. Elles constituent une part importante du rayonnement de la plupart des corps incandescents (cf. chap. 3); on les a d’abord étudiées presque uniquement d’après leurs effets thermiques, mais elles agissent aussi sur certains récepteurs photoélectriques tels que les alliages semiconducteurs III-V et II-VI, en plein essor; elles jouent aujourd’hui un rôle important en analyse chimique par spectrophotométrie, ainsi que pour les télécommunications optiques (cf. TÉLÉCOMMUNICATIONS – Télécommunications optiques), la détection de corps chauds (objectifs militaires, êtres vivants...) et pour des usages médicaux ou industriels, tels que la mesure très sensible des températures superficielles.

L’observation des phénomènes de réflexion, de réfraction, d’interférences et de polarisation dans les régions du spectre électromagnétique de fréquences inférieures à celles du domaine visible a joué un rôle important dans l’assimilation des idées de l’électromagnétisme par la communauté des physiciens. Citons, à ce sujet, les expériences de Hertz (1888) dans le domaine métrique et le raccord de l’infrarouge aux ondes hertziennes. La différence de comportement des détecteurs est cependant très importante selon la fréquence: aux fréquences supérieures à environ 10¹¹ Hz, tous les détecteurs connus sont sensibles à l’énergie, c’est-à-dire à la moyenne temporelle du carré des champs de l’onde électromagnétique et, pour les basses fréquences, on dispose de détecteurs capables de suivre instantanément les variations. Cette distinction permet de séparer le domaine de la lumière et de l’optique de celui de l’électricité et de l’électronique.

L’extrémité du spectre visible, du côté du violet, est aussi mal définie que du côté du rouge. On convient souvent d’adopter, pour limites de l’ultraviolet (subdivisé arbitrairement comme l’infrarouge), les valeurs 400 et 13,6 nm. Le spectre solaire s’arrête pratiquement vers 300 nm, les radiations de longueurs d’onde plus courtes étant absorbées par l’atmosphère. Mais d’autres sources: arcs, étincelles, lampes à décharge (à enveloppe de quartz), placées au besoin dans le vide et associées à des récepteurs photographiques ou photoélectriques convenables, ont permis de pousser l’exploration bien au-delà.

L’arc au mercure est une source très souvent utilisée de rayons ultraviolets; en arrêtant par un filtre convenable (verre au nickel) les radiations visibles, on obtient une «lumière de Wood» (dite parfois, très improprement, «lumière noire»).

L’aptitude de certaines radiations ultra-violettes à faciliter diverses réactions les a fait parfois qualifier de chimiques, alors que les radiations infrarouges étaient dites thermiques. Mais on ne doit pas oublier que ce dernier qualificatif est applicable à n’importe quel rayonnement électromagnétique, puisque tous transportent de l’énergie, qui est transformable en chaleur.

Les rayons X, qui sont émis par la matière subissant le choc d’électrons très rapides, furent ainsi dénommés parce que, lors de leur découverte par Roentgen (1895), leur nature paraissait mystérieuse (cf. rayons X). On a reconnu par la suite qu’ils subissent, dans des conditions bien choisies, des déviations par réflexion, par réfraction, par diffraction (sur des cristaux). Ce sont des radiations électromagnétiques, mais leurs longueurs d’onde sont très faibles (de 1,2 à 0,01 nm), pour ceux qu’on obtient le plus aisément par bombardement électronique. Le rayonnement synchroton émet un spectre continu des rayons X au domaine visible.

Rappelons enfin que les rayons 塚 émis par les corps radioactifs et qu’une partie des rayons cosmiques sont encore de même nature, avec des longueurs d’onde pouvant atteindre près de 0,1 nm et descendre bien au-dessous de 10^-5 nm. On s’en tiendra toutefois, dans ce qui suivra, à considérer comme «lumières» (visibles ou non) les radiations dont l’ensemble s’étend des rayons X à l’infrarouge lointain.

3. L’émission des radiations

Les objets éclairés, comme la Lune, les nuages, le ciel diurne..., qui ne font que diffuser (par réflexion ou transmission) la lumière reçue, constituent des sources de lumière «secondaires». Cette diffusion se fait sans changement de fréquence, sauf cas exceptionnels (cf. effet RAMAN). La plupart des sources lumineuses sont formées de solides incandescents: c’est le cas du Soleil, des flammes chargées de particules de charbon, des lampes à filament de tungstène, des arcs au carbone, etc. Leur lumière est à spectre continu, sa composition variant avec leur nature et leur température.

Des décharges électriques dans un gaz interviennent dans les lampes à vapeur de mercure ou de sodium, les étincelles et certains arcs. Si la pression du gaz n’est pas trop forte, ces sources ont un spectre de raies, ce qu’on peut obtenir aussi (mais avec une faible luminance) en introduisant, dans une flamme non éclairante, un composé minéral, du sel marin par exemple (fig. 3).

Les spectres de raies (ou de bandes) sont caractéristiques des sources qui les produisent. Les recherches à leur sujet ont fourni, depuis le début du XX^e siècle, des résultats très importants, dont l’interprétation combinée avec celle des phénomènes d’ionisation et de transmutation, a conduit aux théories actuelles de la matière et du rayonnement. En outre, une fois connu (tout au moins quant à ses principales raies ou bandes) le spectre d’une substance, il est possible, par un examen spectroscopique, de l’identifier dans un mélange. Cette analyse spectrale peut être extrêmement sensible, une proportion relative inférieure à 10^-7 étant, dans certains cas, décelable.

L’émission de rayonnement par des substances prises dans un état physique quelconque se produit lorsqu’elles sont soumises à des excitations convenables: chocs atomiques intervenant à des températures assez élevées ou sous l’action de champs électriques intenses, ou bien absorption d’autres rayonnements électromagnétiques. On dit qu’il y a incandescence quand l’énergie rayonnée a une origine purement thermique, luminescence dans les autres cas; on peut distinguer, notamment, ceux d’électroluminescence, de triboluminescence (craie ou sucre que l’on broie), de chimiluminescence (oxydation lente du phosphore), de bioluminescence (ver luisant) et, surtout, de photoluminescence.

Spectres d’émission

Le cas d’émission dont l’étude est la plus simple est celui des gaz monoatomiques, où les atomes sont assez éloignés les uns des autres pour qu’il n’y ait pas d’interaction entre eux. Leurs spectres se situent presque toujours dans le visible et l’ultraviolet. On sait que chaque atome est formé d’un noyau, entouré d’un nombre Z d’électrons qui caractérise son espèce chimique (cf. ATOME et classification PÉRIODIQUE).

Les mouvements des électrons autour des noyaux correspondent à des énergies atomiques dont les valeurs possibles, en régime dit stationnaire, sont en nombre limité. Cela apparaît, par exemple, dans les expériences sur l’excitation des atomes par chocs électroniques, où l’énergie qui sert au rayonnement est absorbée par quantités discontinues. On peut se représenter les électrons comme répartis suivant des couches ou niveaux qu’on désigne par les lettres K, L, M... La couche K, la plus voisine du noyau, ne peut contenir que deux électrons, la couche L, un peu plus éloignée, n’en peut contenir que 8, etc. (Ces couches se subdivisent en sous-niveaux voisins.) On appelle état fondamental celui qui correspond au niveau énergétique le plus faible, l’ensemble des électrons se trouvant alors le plus près possible du noyau.

On sait que l’idée d’identifier les fréquences des radiations émises par les sources de lumière à celles des mouvements des électrons a dû être abandonnée. Les effets d’excitation doivent correspondre au passage d’un niveau énergétique à l’un des niveaux supérieurs possibles, et c’est, comme l’a admis Bohr (1913), seulement lors d’un passage inverse que se produit l’émission d’un photon.

Sa fréquence 益 est telle que:

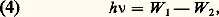W ¹ et W ² étant les niveaux d’énergie atomique avant et après l’émission. Leur étude a montré que les électrons, dits optiques, «responsables» des émissions de lumière visible ou proche du domaine visible, sont ceux de la couche externe (la plus éloignée du noyau) occupée dans l’état fondamental (au moins partiellement, les autres l’étant en général complètement). Ces électrons sont les mêmes que les électrons de valence, intervenant dans les liaisons chimiques: plus leur nombre est élevé et plus le spectre se complique.

Spectres d’absorption

Indépendamment d’une absorption continue, liée à la conductivité dans la théorie électromagnétique, beaucoup de corps absorbent sélectivement la lumière qu’ils reçoivent. En les interposant sur le parcours d’un rayonnement à spectre continu, on fait apparaître dans ce spectre des raies ou bandes sombres, dues à l’absorption. Celle-ci correspond à une excitation des atomes, dont le retour à un niveau inférieur peut avoir lieu soit par réémission de lumière, soit par perte d’énergie sous une autre forme: agitation thermique, réactions chimiques... Les fréquences ainsi absorbées obéissent, bien entendu, à la formule (4).

Dans les spectres d’absorption ou d’émission, les raies peuvent être groupées en «séries» (fig. 4) dont chacune correspond à un même niveau énergétique final. Quand un atome est ionisé, ses niveaux, et par suite ses spectres, diffèrent de ce qu’ils sont pour l’atome neutre.

Spectres et structures atomiques

On trouvera dans l’article SPECTROSCOPIE des données sur les structures atomiques, déduites de l’étude des spectres, ainsi que sur les modifications que peuvent subir les raies : déplacement lorsque la source est en mouvement par rapport à l’observateur (effet Doppler), division en plusieurs composantes, sous l’action d’un champ magnétique (effet Zeeman) ou électrique (effet Stark), élargissement quand la température ou la pression s’élèvent. Leur interprétation présente un grand intérêt théorique; elle a fourni, en particulier, combinée avec l’analyse chimique spectrale, la plus grande part de nos connaissances sur les étoiles.

Émission des rayons X

On trouvera dans l’article rayons X, des indications sur les fréquences qui constituent ces rayonnements et sur la façon dont ils sont absorbés. Signalons seulement que, s’ils sont produits par l’impact d’électrons (de charge e ), accélérés sous une tension V , le quantum maximal h 益 émis peut être au plus égal à l’énergie cinétique (eV ) des électrons, d’où la condition 益 諒 eV /h (soit 2,42 . 10¹⁴ V, si 益 est évalué en hertz et V en volts). Le spectre d’émission comporte, jusqu’à cette limite, un fond continu dû au fait que l’électron perd son énergie par fractions quelconques, au cours d’un nombre variable de collisions, l’accélération négative qui en résulte s’accompagnant d’une émission de fréquence variable: de tels rayonnements de freinage se retrouvent pour la production de rayons 塚 et sont expliqués par une théorie relativiste.

Le rayonnement de freinage n’est qu’une illustration de la loi générale selon laquelle toute charge électrique en mouvement accéléré émet un rayonnement électromagnétique. Ainsi, les particules chargées des accélérateurs constituent une source intense de lumière à spectre très large. En particulier, dans la plupart des grands centres mondiaux de physique des hautes énergies, les électrons tournant dans les anneaux synchrotrons sont utilisés depuis plusieurs années comme sources lumineuses; le rayonnement synchrotron se présente sous la forme d’un mince rideau de lumière à très grande intensité. La figure 5 présente le spectre émis par le synchrotron Superaco, construit à Orsay spécialement en tant que source lumineuse.

Au fond continu se superposent des raies caractéristiques des atomes émetteurs, qu’ils soient libres ou combinés. Leur quantum élevé nécessite non plus l’intervention des électrons de valence, comme pour les spectres «optiques», mais celle des électrons plus fortement liés dans l’atome, donc appartenant aux couches les plus voisines du noyau. Le mécanisme admis est le suivant: l’énergie reçue par l’atome l’ionise, c’est-à-dire arrache de la couche K, par exemple, un électron qui ne peut se fixer sur les couches extérieures L, M, N déjà «remplies». Mais un électron d’une de ces couches peut venir prendre la place ainsi laissée vacante, avec une émission de fréquence donnée par la formule (4). Les raies X sont par suite classées en séries, que l’on a désignées par les lettres K, L, M... correspondant aux niveaux d’arrivée, celles d’une même série se distinguant, suivant le niveau de départ, par des indices 見, 廓, ... (avec des dédoublements résultant de niveaux multiples, fig. 6).

Contrairement aux spectres optiques, les spectres X des divers éléments ont tous sensiblement le même aspect. Une loi approchée, établie empiriquement par Moseley et justifiée théoriquement, indique, en particulier, que la fréquence de la raie K size=1^見 varie en raison inverse de (Z 漣 1)², Z étant le numéro atomique. Cette loi a apporté, lors de sa découverte, une confirmation précieuse à la classification de Mendeleïev.

Les spectres d’absorption X ne présentent pas de raies (en raison de l’impossibilité d’un saut électronique inverse de celui qui est lié à l’émission), mais des discontinuités (fig. 6) correspondant aux possibilités d’ionisation successives des électrons K, L, M... lorsque le quantum absorbé augmente.

Spectres moléculaires

Lorsque les spectres optiques sont émis ou absorbés non plus par les atomes, mais par les molécules, supposées indépendantes les unes des autres, ils sont en général formés de raies, mais beaucoup plus nombreuses; elles sont le plus souvent groupées en bandes, à l’intérieur desquelles elles peuvent être séparées par un appareil spectroscopique de résolution suffisante (fig. 7). Ces raies se localisent en trois régions principales: ultraviolet ou visible, infrarouge proche ou moyen, infrarouge lointain ou ultra-hertzien. Dans ce dernier cas, les sauts d’énergie qui les provoquent sont relativement faibles et correspondent à des variations discontinues des états de rotation de l’ensemble de la molécule. Lorsque les sauts d’énergie sont plus importants, ces rotations sont combinées avec des vibrations possibles des noyaux; enfin, les quanta les plus élevés résultent des mouvements périphériques des électrons. L’étude de ces spectres, faite le plus souvent en absorption, se prête très utilement à des identifications et à des recherches sur les structures moléculaires.

Spectres des corps à l’état condensé

Le passage des corps à l’état condensé (gaz comprimés, liquides, solides) s’accompagne de changements souvent importants, dus aux interactions moléculaires, pour leurs spectres d’émission et d’absorption: beaucoup de niveaux d’énergie sont moins bien définis, et les raies correspondantes s’élargissent et se soudent en formant des bandes qui ne sont pas résolubles. Pour les cristaux, toutefois, l’entourage de chaque atome est plus régulier, et les spectres sont mieux détaillés que pour les mêmes corps à l’état liquide.

Incandescence

Le spectre continu des corps incandescents non gazeux résulte d’un très grand nombre d’excitations par chocs des atomes ou molécules, dont l’agitation thermique augmente avec la température. Une enceinte fermée à température uniforme, qu’on appelle un corps noir , représente un cas particulier d’incandescence. La lumière qu’elle rayonne par une très petite ouverture a une intensité proportionnelle à la surface de celle-ci, mais elle ne dépend pas de la nature de l’enceinte: aussi parle-t-on du corps noir, et non des corps noirs. Les lois de son rayonnement sont bien établies et relativement simples ^{[cf. PHOTOMÉTRIE]}.

Un corps noir absorbe toute l’énergie rayonnante qu’il reçoit (d’où son nom). Tout autre corps incandescent absorbe, pour une longueur d’onde donnée, une fraction 見 諒 1 de l’énergie incidente; Kirchhoff a montré (1860) que son rayonnement est, quel que soit son état physique, dans un rapport 見 avec celui du corps noir, à la même température et pour la même longueur d’onde. Les corps les plus absorbants, tels que le carbone pour les radiations visibles, sont donc ceux dont le rayonnement purement thermique est le plus intense. Mais cette loi ne s’applique pas aux cas de luminescence.

Luminescence

Parmi les cas de luminescence, examinons les cas de photoluminescence , où l’excitation est produite par le champ électrique d’une onde lumineuse absorbée. Une substance exposée à un faisceau X convenablement choisi peut réémettre des rayons X, qui sont alors qualifiés de «secondaires ». Mais le phénomène est surtout intéressant dans les cas d’émission de radiations visibles par certains corps recevant une lumière d’assez courte longueur d’onde.

La photoluminescence est interprétée comme l’absorption d’un photon amenant un électron du matériau éclairé à un niveau quantique d’énergie supérieure, suivie d’émission lumineuse lors de la désexcitation. Il existe trois cas de photoluminescence:

– la résonance optique , qui correspond à la réémission de la fréquence absorbée par désexcitation directe du niveau supérieur au niveau fondamental; un exemple bien connu en est l’excitation lumineuse et la réémission diffuse du doublet D des alcalins;

– la fluorescence , qui fait intervenir une désexcitation partielle non radiative du niveau supérieur, instable, à un niveau intermédiaire, lui-même instable, suivie de la désexcitation lumineuse jusqu’au niveau fondamental, dont la fréquence est nécessairement inférieure à la fréquence excitatrice; elle se manifeste en un temps très court, de l’ordre de 1 ns, après l’absorption; la couleur verte de la fluorescéine éclairée en lumière blanche (dont la partie bleue est absorbée), l’émission violacée de nombreux tissus ou papiers éclairés en ultraviolet en sont des exemples courants;

– la phosphorescence , qui fait également intervenir un niveau intermédiaire, mais métastable: ce cas se produit dans des cristaux comme les sulfures alcalins ou alcalino-terreux, qui contiennent une quantité convenable d’impuretés métalliques créatrices de pièges; l’émission, dite de phosphorescence, est d’une fréquence inférieure à la fréquence excitatrice, elle suit donc l’absorption avec un délai long et sensible aux conditions extérieures; un réchauffement active la phosphorescence, en favorisant par agitation thermique la sortie de l’électron de son état métastable, un refroidissement gèle cette phosphorescence; un faisceau infrarouge peut également éjecter l’électron de son piège.

Les applications de la luminescence des solides sont de plus en plus nombreuses: en éclairagisme, pour des effets publicitaires ou théâtraux, pour le revêtement d’écrans sensibles aux rayons ultraviolets, aux rayons X (platinocyanure de baryum) et aux faisceaux électroniques (récepteurs de télévision). Dans l’éclairage par luminescence , une décharge dans un tube contenant de la vapeur de mercure à basse pression lui fait émettre principalement une raie (de résonance) ultraviolette. La partie interne du tube est enduite d’une poudre présentant une phosphorescence de courte durée (silicate de zinc, tungstate de calcium, etc.); des mélanges convenables de ces substances permettent d’obtenir des lumières visibles de nuances variées, en particulier se rapprochant de la lumière du jour. Le rendement lumineux est sensiblement supérieur à celui des lampes à filament incandescent.

Lasers

Les lasers utilisent un cas particulier de fluorescence, dans lequel l’émission de lumière de fréquence 益 par des atomes excités, qui est habituellement «spontanée» et produite au hasard, se trouve (comme l’avait envisagé Einstein dès 1917) «stimulée» par des photons de même fréquence, ceux-ci n’étant pas absorbés.

Ils produisent une amplification de lumière, qui n’est toutefois possible que si les atomes amenés à l’état excité sont plus nombreux que ceux de l’état inférieur, ce qui ne se produit pas naturellement et exige ce qu’on appelle une inversion de population (cf. LASERS).

Seul, le laser à électrons libres ne nécessite pas une telle inversion; il tire ses propriétés de l’accord de phase entre l’onde amplifiée et les oscillations transversales périodiques, forcées d’électrons relativistes dont la trajectoire traverse une région où une distribution régulière d’aimants produit un champ magnétique déflecteur approprié.

Le grand intérêt des lasers tient à ce qu’ils permettent de concentrer sur une surface très petite, et en un temps très court, un flux lumineux très intense, et surtout à ce que leurs faisceaux sont remarquablement «cohérents». L’onde émise se trouve, en effet, en accord de phase avec celle qui la stimule, alors qu’il n’y a aucune relation de phase déterminée entre les ondes émises spontanément, au hasard, par des atomes excités.

Les «trains d’onde» lasers sont, par suite, beaucoup plus longs que ceux des autres sources de lumière; on dit que la lumière d’un laser présente une grande cohérence longitudinale, ou encore temporelle (cet adjectif traduisant la durée des trains d’onde). Elle a aussi une grande cohérence spatiale (ou transversale), ce qui veut dire que des points situés à une certaine distance l’un de l’autre (des millimètres), normalement à la direction de propagation, sont encore en accord de phase. Elle permet donc d’observer des interférences à différences de marche beaucoup plus grandes que celles que l’on obtient à l’aide des autres lumières.

4. Les récepteurs de lumière

L’étude des lumières, isolées au besoin par des dispositifs spectrométriques, se fait à l’aide de récepteurs dont on indiquera les caractéristiques essentielles (sans insister sur les transformateurs photoluminescents déjà considérés). Les récepteurs sont dits thermiques, photoélectriques, photochimiques selon la forme d’énergie en laquelle ils transforment l’énergie rayonnante qu’ils reçoivent. Les premiers ont l’intérêt de ne pas être sélectifs, c’est-à-dire que leur réponse est, à puissance constante, indépendante de la composition spectrale de l’énergie absorbée. Ils se prêtent donc à l’étalonnage des autres récepteurs, qui sont sélectifs, mais beaucoup plus sensibles, pour certaines fréquences. Les récepteurs perçoivent le flux reçu par leur surface sensible (ou par les surfaces sensibles de chacun de leurs éléments).

La rétine

La rétine , organe intermédiaire entre les éléments transparents de l’œil et le nerf optique, est un récepteur photochimique, mais de nombreux facteurs, d’ordre physiologique et même psychologique, conditionnent la perception visuelle, qui présente donc un caractère subjectif. Les récepteurs physiques, c’est-à-dire autres que l’œil, peuvent au contraire fournir des informations objectives, et leur domaine s’étend bien en dehors du spectre visible.

La figure 1 de l’article COULEUR représente (en valeurs relatives, ramenées au même maximum pris pour unité) la sensibilité aux diverses radiations monochromatiques (à puissance constante) d’un œil «moyen», conventionnellement défini à partir d’études statistiques. Celle de chaque individu peut s’en écarter sensiblement, elle varie d’ailleurs avec l’âge, la fatigue, l’adaptation à tel ou tel éclairage (même en laissant de côté les cas d’éblouissement). La longueur d’onde à laquelle l’œil est le plus sensible se situe vers 0,55 猪m (couleur vert-jaune) en vision diurne; mais une exposition assez longue (des dizaines de minutes) aux faibles éclairements l’abaisse vers 0,51 猪m, l’œil devenant alors relativement plus sensible au bleu qu’au rouge (effet Purkinje). L’évaluation de ces sensibilités suppose évidemment que l’on sait comparer visuellement des lumières de couleurs différentes ^{[cf. PHOTOMÉTRIE]}. On admet que, dans un faisceau complexe, les effets des divers constituants s’ajoutent, au moins approximativement. Il existe, d’ailleurs, un seuil de perception au-dessous duquel l’œil ne voit plus rien; très variable selon les observateurs et les objets qu’ils regardent, il peut s’abaisser en deçà de 10^-15 watt pour la vision nocturne d’une source ponctuelle de longueur d’onde optimale.

Une autre caractéristique de l’œil, intéressante en particulier pour son emploi avec des instruments d’observation, est son aptitude à distinguer des images plus ou moins écartées angulairement: cette limite de séparation (pouvoir de résolution) est de l’ordre de une à deux minutes d’angle pour des bandes équidistantes noires et blanches de même largeur; elle est notablement plus grande aux faibles luminances et aux faibles contrastes ^{[cf. VISION]}.

Récepteurs thermiques

Les récepteurs thermiques sont, le plus souvent, des thermomètres très sensibles, à couples, à variation de résistance ou à augmentation de pression d’un gaz. Ils doivent avoir une faible capacité calorifique et être noircis de façon à absorber le mieux possible le rayonnement qui tombe sur eux. Ils s’échauffent jusqu’à ce que la chaleur qu’ils rayonnent eux-mêmes ou qu’ils perdent par conduction et convection compense exactement celle qu’ils gagnent par absorption. En régime permanent, atteint plus ou moins vite, leur très faible excès de température (on peut déceler 10^-5 degré) par rapport au milieu qui les entoure indique, en valeur relative et parfois en valeur absolue, la puissance rayonnante qu’ils reçoivent.

Leur réponse étant plus faible que celle des autres récepteurs, ils servent essentiellement à établir les courbes de sensibilité spectrale de ces derniers. Ce sont les seuls utilisables pour certaines mesures dans l’infrarouge: si l’on dispose souvent d’une puissance plus grande que dans le visible et l’ultraviolet, les récepteurs photographiques et photoélectriques n’ont aucune sensibilité pour les grandes longueurs d’onde.

L’étalonnage d’un récepteur thermique se fait soit d’après sa réponse au rayonnement d’un «corps noir» à température connue, soit en apportant un débit de chaleur connu (par un courant électrique, par exemple). On doit s’appliquer à tenir compte, dans chaque mesure, des valeurs du facteur d’absorption de la surface noircie (généralement inférieures à l’unité dans l’infrarouge) et, s’il y a lieu, des pertes de lumière incidente dues à l’absorption par l’air.

Les thermocouples produisent, par échauffement, une force électro-motrice V proportionnelle à la puissance W reçue par l’une des soudures joignant deux métaux disposés en série; on mesure V (des fractions de microvolts) à l’aide d’un galvanomètre, la résistance électrique R du circuit étant constante et faible (de quelques ohms à quelques dizaines d’ohms). Les métaux sont, par exemple, du cuivre et du constantan, ou du bismuth et un alliage bismuth-étain. La surface noircie est juste suffisante pour recevoir le faisceau à mesurer; la soudure (dite froide) à l’abri du rayonnement et celle qui y est exposée sont disposées de façon à être influencées de la même façon par les variations de la température ambiante. Certains thermocouples sont placés dans le vide, pour supprimer les pertes de chaleur par convection (fig. 8). Très souvent, les soudures sont multiples, l’emploi de plusieurs thermocouples en série augmentant V (pour un même éclairement) plus que la résistance R de l’ensemble. La mise en équilibre demande un temps proportionnel à la sensibilité du thermocouple (de moins de 0,1 s à plus de 1 s).

Les bolomètres sont de petites lames de platine ou de nickel, ou mieux des mélanges d’oxydes semiconducteurs (thermistances), dont la variation de résistance électrique provoque, dans un circuit convenable, un courant proportionnel à l’échauffement. La durée de mise en équilibre et la sensibilité (déviation d’un galvanomètre par microwatt de puissance reçue) sont comparables à celles des thermocouples.

D’excellents récepteurs, dits pneumatiques , ont été constitués en mettant la surface appelée à recevoir le rayonnement au contact d’un gaz enfermé dans une petite enceinte; l’augmentation de pression due à l’échauffement provoque sur une légère membrane manométrique une déformation, qui entraîne la variation d’un courant électrique. Ce dispositif ayant une très faible inertie, le flux à mesurer peut être interrompu à une fréquence de 10 à 100 Hz, et les variations alternatives du courant peuvent être amplifiées.

L’effet pyroélectrique se manifeste par l’apparition d’une charge électrique entre les faces d’un cristal placées à des températures différentes. Il se prête à la détection de l’échauffement provoqué par les rayonnements électromagnétiques. Même pour le matériau le plus couramment utilisé, le sulfate de glycocolle, l’effet est si faible que son utilisation pratique requiert une amplification par transistor à effet de champ. Dans ces conditions, l’effet pyroélectrique est intéressant dans le domaine de l’infrarouge «thermique» vers 10 猪m, par exemple pour la thermographie et les systèmes de surveillance. En disposant en ligne quelques dizaines, voire quelques centaines d’éléments pyroélectriques et en superposant quelques dizaines ou centaines de telles lignes, on obtient des détecteurs «matriciels» qui sont disponibles commercialement.

Récepteurs photoélectriques

Certains atomes, en absorbant des lumières convenables, émettent des électrons (cf. effet PHOTOÉLECTRIQUE). Ce phénomène est comparable, en sens inverse, à l’émission de rayons X sous l’action de chocs électroniques. Il est encore réglé par une loi quantique, mais ici l’énergie h 益 du photon doit être au moins égale à un certain «travail d’arrachement», W , des électrons, la différence h 益 漣 W étant communiquée à ceux-ci sous forme cinétique. Ne sont donc actifs que les photons de longueur d’onde 諒 h 益/W ⁰ (W ⁰ étant la valeur minimale de W ), ce qui détermine un «seuil photoélectrique»⁰: il peut se trouver, selon le cas, dans l’ultraviolet, le visible, et même le début de l’infrarouge.

La figure 9 représente schématiquement un type de cellule photoémissive : c’est une ampoule, souvent vide de gaz, où le flux, pénétrant par une fenêtre, tombe sur une cathode C reliée au pôle négatif d’une pile; l’anode A (de forme cylindrique ou annulaire, ou constituée par une grille) est portée par rapport à C à un potentiel positif V ; elle capture les électrons, dont le débit est mesuré par le galvanomètre G. Si V atteint une valeur suffisante (des volts ou des dizaines de volts, selon le type de cellule), cette capture est totale, et le courant i atteint une valeur de saturation proportionnelle à 淋. La sensibilité i / 淋 (nulle pour 礪⁰) varie avec la nature de la cathode et la composition spectrale du flux reçu.

Le courant s’établit ou cesse en même temps que l’éclairement reçu, même si celui-ci est très faible (ce qui a fourni en faveur de la théorie quantique un argument analogue à celui qui est indiqué par les expériences sur le noircissement photographique).

Dans le domaine visible, les antimoniures alcalins sont les matériaux les plus utilisés pour les photocathodes. Si la cellule photoémissive a joué un rôle historique important, elle est actuellement peu utilisée, mais l’effet dont elle a été le révélateur est mis à profit dans des dispositifs très variés dont l’évocation suit.

Une cellule photomultiplicatrice , telle que celle qui est représentée schématiquement sur la figure 10 (il en existe d’autres types), comporte entre la cathode C, qui reçoit le flux étudié, et l’anode A des électrodes intermédiaires (G¹, G², G³...) portées à des potentiels de plus en plus élevés par rapport à C. L’augmentation d’énergie cinétique de l’une à l’autre leur permet d’arracher au métal des «électrons secondaires», qui agissent de même sur les électrodes suivantes; c’est ainsi que des gains de plus d’un million d’électrons ont pu être obtenus.

L’effet photoélectrique interne est observé dans les semiconducteurs, où le photon absorbé fournit à un électron l’énergie nécessaire pour passer de la bande de valence à la bande de conduction. Il se manifeste au niveau de jonctions entre semiconducteurs et conducteurs par l’apparition d’une force électromotrice utilisée dans les photopiles , au niveau de jonctions p-n par l’apparition d’une charge dans les photodiodes , et dans les semiconducteurs massifs par la diminution de la résistivité des cellules photoconductrices .

La figure 11 représente schématiquement une photopile; elle comporte un disque métallique D (en fer, dans le cas considéré), constituant l’un des pôles, recouvert d’une couche semiconductrice S (sélénium), sur laquelle se trouve un dépôt métallique M (platine ou or), assez mince pour rester transparent au flux 淋; un anneau métallique A en contact avec ce dépôt forme le second pôle de la pile. Le courant débité peut être de l’ordre du milliampère par lumen – pour la lumière du jour ou celle des lampes usuelles –, sans qu’il soit besoin, comme dans les cellules photoémissives, d’une source extérieure. Très utilisés en photométrie courante, notamment dans les posemètres photographiques (malgré une fidélité parfois médiocre), ces récepteurs constituent les éléments des piles solaires dont l’emploi, courant dans les engins spatiaux, s’est développé également sur Terre.

Les photodiodes, ainsi que les phototransistors qui font appel aux mêmes techniques et dépassent ces dernières en sensibilité, sont d’un emploi de plus en plus fréquent grâce aux performances de la technologie des semiconducteurs qui permettent de disposer de détecteurs utilisables avec un bon rendement, de l’ultraviolet moyen à l’infrarouge moyen (200 nm à 4 猪m environ), couvrant notamment la bande spectrale habituelle des télécommunications optiques. Des détecteurs au silicium multiples arrangés en «matrices» de plus de 1 000 lignes comportant chacune plus de 1 000 photodiodes ou phototransistors sont disponibles commercialement: leur faible encombrement et leurs bonnes performances leur permettent par exemple de remplacer avantageusement les tubes de prise de vue de télévision (fig. 12).

Les cellules photoconductrices, nécessitant une polarisation électrique, sont le siège d’un bruit de détecteur qui limite leur emploi aux domaines de longueurs d’onde où les autres dispositifs photoélectriques ne conviennent pas, c’est-à-dire l’infrarouge de 3 à 100 猪m environ.

Récepteurs photochimiques

Les conditions du noircissement des émulsions photosensibles sont étudiées à l’article PHOTOGRAPHIE. Ces émulsions ont l’intérêt de permettre, en augmentant le temps de pose, d’accumuler les effets du rayonnement, donc d’apprécier un faible éclairement, mais elles se prêtent aussi, quand ce dernier est suffisant, à l’enregistrement de lumières brèves ou rapidement variables. Leur sensibilité peut déborder largement le spectre visible (fig. 13); seules utilisées dans l’ultraviolet, avant l’emploi des cellules photoélectriques, elles rendent aussi, moyennant une composition convenable, des services dans le proche infrarouge.

Les matériaux photochromiques , dont certains sont connus depuis longtemps, sont actuellement l’objet d’un intérêt accru. Leur changement de couleur ou d’opacité sous l’action d’une lumière convenable est réversible, le retour à l’état primitif se faisant «naturellement» dans l’obscurité (parfois lentement, mais d’autant plus vite que la température est plus élevée), ou encore sous l’action de photons de longueurs d’ondes différentes de celles qui ont produit l’«activation». Celle-ci peut être due à une modification chimique, à une excitation ou ionisation, à un déplacement d’électrons dans un réseau cristallin... Parmi les matériaux utilisables, on peut citer, par exemple, des cristaux de fluorure de calcium – «dopés» par des éléments des terres rares –, des verres contenant des particules d’halogénures d’argent, des films comportant une solution homogène de corps organiques, tels que certains spiropyrannes.

L’effet maximal est atteint (par exemple) au bout de quelques dizaines de secondes à la lumière directe du Soleil (on l’utilise dans certaines lunettes solaires) et de 10^-5 s pour les éclairements les plus intenses (protection contre la lumière des explosions nucléaires). Pour l’enregistrement d’images ou de signaux (holographie, mémoires optiques...) relativement peu lumineux, les récepteurs photochromiques demandent un temps de pose bien plus long que les émulsions photographiques, mais évitent l’opération de développement d’une image latente.

En plus de son intervention dans la vision, la lumière a des effets biologiques de la plus grande importance: la vie humaine est possible en l’absence du sens de la vue, mais elle ne le serait pas sans l’intervention du rayonnement et, tout spécialement, sans celle de l’énergie qui vient du Soleil. Cette énergie, par sa transformation en chaleur, permet le maintien de la température à la surface de la Terre, la formation des nuages (d’où la «houille blanche») et aussi, par l’intermédiaire de réactions photochimiques , la nutrition de presque tous les végétaux (d’où les combustibles divers), et par suite celle des animaux.

5. Vitesse de la lumière

On a cru longtemps que l’action de la lumière à distance se produisait instantanément. Les premières expériences à ce sujet ont eu surtout pour effet de montrer que sa vitesse de propagation n’est pas infinie et qu’elle est constante dans un milieu, pour une longueur d’onde donnée; on s’est ensuite attaché à déterminer les variations de cette vitesse selon le milieu et à préciser sa valeur dans le vide, dont la connaissance a un grand intérêt théorique et pratique.

La vitesse de la lumière dans le vide est identique pour toutes les ondes électromagnétiques, quelle que soit leur fréquence; cette constante est notée c (d’après le mot célérité). Dans tout autre milieu, cette vitesse dépend de la fréquence: c’est le phénomène de dispersion. Une vibration lumineuse se propageant dans un milieu dispersif sous la forme d’une onde plane monochromatique de fréquence 益 dans la direction et le sens positif de l’axe Ox peut s’écrire:

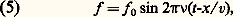où v, appelée vitesse de phase, permet de définir l’indice de réfraction N du milieu pour la fréquence 益 par la relation N = c /v. Mais, en raison des variations de la vitesse de phase avec la fréquence, toute onde non monochromatique, en se propageant, se déforme, ce qui rend la définition de l’expression «vitesse de la lumière» difficile. Il est d’usage de distinguer de la vitesse de phase la vitesse de groupe:

Cette vitesse de groupe représente la vitesse de déplacement du maximum de l’enveloppe d’un «train d’onde», ou «paquet d’ondes», constitué de la superposition d’ondes monochromatiques très voisines. Dans les milieux dispersifs transparents, v^g peut être assimilé avec une bonne approximation à la vitesse de déplacement de l’énergie ou du signal transportés par un tel paquet d’onde. Dans les milieux absorbants ou en présence d’ondes à spectre très large, un calcul complet de la propagation de l’énergie à l’aide des équations de Maxwell s’impose.

Léon Foucault (1851), par une expérience directe, établit que la vitesse de la lumière est plus faible dans l’eau que dans le vide; dans le cas où le corps éclairé est en mouvement à la vitesse v dans la même direction que la lumière par rapport au laboratoire, il vérifia que l’effet Doppler longitudinal porte la vitesse de phase à: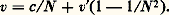

Cette dernière valeur, déjà prévue par Fresnel, est en excellent accord avec la relativité.

Mesure de c

La mesure de c doit être effectuée dans le vide à moins de résulter de mesures séparées de v et de N . Par exemple, l’indice de l’air aux températures et pressions usuelles pour la lumière visible étant voisin de 1,000 3, une correction s’impose dès que la précision relative sur c atteint quelques dix-millièmes.

La première détermination «astronomique» fut faite en 1676 par Olaüs Römer. La planète Jupiter (J, sur la figure 14) possède plusieurs satellites, tels que L, qui pénètrent dans son ombre à chaque révolution. Mais l’intervalle entre deux éclipses successives paraît tantôt un peu plus court que la moyenne des valeurs mesurées sur un très grand nombre d’éclipses, tantôt un peu plus long. Römer expliqua ainsi cette variation: les éclipses sont bien des signaux partant de Jupiter à intervalles sensiblement égaux, mais l’espace qu’il leur faut parcourir pour atteindre la Terre diminue d’une éclipse à la suivante quand les deux planètes se rapprochent l’une de l’autre, augmente dans le cas contraire.

Quand la Terre passe de ¹ à ³ (ce qui demanderait exactement une demi-année, si Jupiter ne tournait pas lui aussi autour du Soleil S), les avances de temps considérées ci-dessus s’accumulent, leur somme étant de l’ordre de 22 minutes. On trouve un temps sensiblement égal pour la somme des retards observés quand la Terre passe de ³ à ¹. Ce temps t est celui qui est mis par la lumière pour parcourir le diamètre l de l’orbite terrestre, soit environ 300 millions de kilomètres.

Les évaluations déduites des mesures de Römer étaient peu précises (il annonça pour c environ 214 000 km/s).

En 1728, un autre astronome, J. Bradley, découvrit un mouvement apparent annuel des étoiles sur la sphère céleste (aberration ), qu’il expliqua par la coexistence d’une vitesse non nulle w de la Terre sur son orbite et d’une vitesse de la lumière c , qu’il fut ainsi possible d’évaluer. Raisonnons, pour simplifier, sur une étoile E dont la direction est supposée normale au plan de l’écliptique et soit l sa distance à la Terre (fig. 15). Pendant le temps t = l /c , mis par la lumière pour venir de l’étoile jusqu’à la Terre, un observateur terrestre est entraîné de A en B, tel que AB = wt . L’axe de la lunette, qui devrait être orienté parallèlement à BE si la Terre était immobile, doit donc l’être parallèlement à AE. (De même, lorsque des gouttes de pluies tombent verticalement, un observateur se déplaçant horizontalement a l’impression que la pluie tombe obliquement, en provenant d’une direction située en avant de lui.)

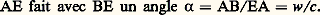Au cours d’une année, la direction de w tourne régulièrement, sa grandeur restant sensiblement la même: la trajectoire apparente de E est donc une circonférence de diamètre angulaire 2 見.

Les mesures donnent approximativement 見 = 20 = 10^-4 radian; la valeur de w (environ 30 km/s) se déduit de celle du contour de l’orbite terrestre, donc, comme dans les calculs de Römer, de la parallaxe solaire. D’où c = w / 見.

On peut remarquer que l’aberration ne dépend pas de la distance l de l’étoile. Elle se superpose à un autre mouvement apparent, de bien moins grande amplitude (variant comme 1/l et toujours inférieur à 1 ), dû aux déplacements relatifs de la Terre et des étoiles relativement proches.

Hippolyte Fizeau, le premier (1849), mesura c par une méthode entièrement terrestre, celle de la roue dentée; la figure 16 donne le schéma du montage qu’il utilisait. D’une source lumineuse S de petites dimensions, la lentille L¹, suivie de la lame semi-réfléchissante l , forme une image au foyer objet F d’une lentille L². Les ensembles de rayons parallèles transmis par L² sont reçus à grande distance par une lentille L³, qui forme une nouvelle image de la source sur le miroir M; ce dernier est orienté normalement à l’axe commun des lentilles L² et L³, que le faisceau réfléchi traverse à nouveau, pour former en F une image finale; l’œil observe celle-ci à travers la lame l et l’oculaire O^c . Une roue R, munie à sa périphérie de p dents identiques régulièrement réparties, est disposée normalement à l’axe du faisceau, de façon que, pendant qu’elle tourne autour de son axe A, F se trouve alternativement soit sur une dent, soit dans l’intervalle (creux) entre deux dents, de même largeur que celles-ci. On règle la vitesse de rotation uniforme q (tours/seconde) de telle sorte que – au bout du temps t = 1/2 pq nécessaire pour qu’une dent prenne la place du creux voisin, ou encore au bout d’un temps (2 k + 1) fois plus grand (k entier) – les faisceaux lumineux issus de S qui ont pu passer à travers les creux successifs défilant en F se trouvent exactement arrêtés par une dent à leur retour. Il faut et suffit, pour cela, que q satisfasse à la condition:

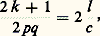l étant la distance MF.

Si l’on fait croître progressivement la vitesse de rotation, l’œil perçoit donc des extinctions de la lumière qu’il reçoit de F, pour des valeurs de q qui sont entre elles comme les nombres impairs successifs. On trouve, par exemple, que pour k = 0 (première extinction), p = 500 et l = 15 km, q doit être voisin de 10 tours par seconde; d’où c . L’incertitude, d’abord grande, fut réduite par la suite à moins de 100 km/s.

On peut considérer comme dérivant de la méthode de Fizeau les mesures relativement récentes utilisant l’effet Kerr (cf. OPTIQUE CRISTALLINE): une cellule contenant du nitrobenzène est placée entre les armatures d’un condensateur, auquel est appliquée une tension alternative de fréquence f . Un faisceau de lumière polarisée rectilignement, traversant cette cellule suivie d’un analyseur, se trouve modulé à une fréquence 2 f , au besoin mille fois plus grande que celle de substitution des pleins aux creux d’une roue dentée. On peut ainsi mesurer c sur un parcours de quelques dizaines de mètres, où l’état de l’air est bien déterminé. Une fois c connu, un montage de ce type peut servir à la mesure précise des distances géodésiques.

La méthode du miroir tournant fut appliquée en 1850 par Foucault (et aussi par Fizeau). En voici le principe (fig. 17): un faisceau issu de la source ponctuelle S tombe à la distance d sur un miroir M tournant à une grande vitesse angulaire 諸 autour d’un axe I de son plan, normal à SI. Il va se réfléchir en I sur le miroir fixe M , qui le renvoie sur lui-même; la distance I I = l est de quelques mètres. Pendant le temps t = 2 l /c , mis par la lumière pour aller de I en I et pour en revenir, M a tourné d’un petit angle 見 = 諸t (radians), de sorte que le faisceau de retour se réfléchit suivant IS , l’angle SIS valant 2 見. D’une mesure de SS = 2 d 見 = 4 諸l d /c , l’on déduit c . Si, par exemple, la rotation se fait à raison de 1 000 tours par seconde, 諸 = 2 000 神 rd/s; pour l = 15 m et d = 10 m, SS est voisin de 12,5 mm.

La méthode permet une mesure dans l’air ou dans un milieu transparent quelconque placé dans un tube (représenté en pointillés sur la figure).

D’autres mesures ont concerné des ondes hertziennes, soit à grande distance (transmission de signaux de Paris à Washington, H. Abraham & G. Ferrié, 1913), soit entre un avion et la Terre, soit le long de fils métalliques, soit encore en mesurant la longueur d’onde (centimétrique) = c /f de fréquence f connue.

La théorie électromagnétique indique aussi que, si l’on confronte les deux systèmes d’unités C.G.S., dits respectivement électrostatique et électromagnétique, utilisés en électricité (cf. ÉLECTRICITÉ – Électromagnétisme), les rapports des unités E.S. et E.M., pour une même grandeur, sont, selon celle-ci, de la forme c et 1/c ou c ² et 1/c ² . Certains de ces rapports ont pu être mesurés avec précision.

Fixation de c

La précision atteinte sur la mesure de c ne peut être supérieure à la précision des phénomènes physiques utilisés dans les définitions des unités de longueur et de temps. Le mètre étalon de 1960 était défini par référence à la longueur d’onde dans le vide d’une transition de l’atome de krypton 86, mais la précision était limitée par la largeur de cette transition. Les lasers, dont les ondes obtenues sont nettement plus monochromatiques, ont permis de donner une définition du mètre beaucoup plus précise. Afin d’éviter d’adopter une nouvelle transition de référence qui risquerait d’être à son tour rapidement caduque, la 17^e Conférence générale des poids et mesures a adopté le 20 octobre 1983 la définition suivante: «Le mètre est la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1/299 792 458 de seconde.» La constante c se trouve maintenant fixée par définition à la valeur 299 792,458 km/s, les méthodes de mesure de c sont transformées en méthodes de mesure de longeur et la précision atteinte sur les mesures de durée en fait potentiellement la mesure de longueur la plus précise qui existe actuellement.

Encyclopédie Universelle. 2012.